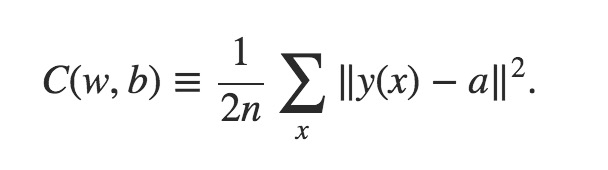有一次,我和Vito(我的合伙人)聊起了当下热门的几种技术趋势。当谈及它们在未来可能的发展前景的时候,Vito说了下面的一段话:
人工智能是个信息革命到蒸汽机规模之间的机会,相比之下虚拟现实应该是移动互联网级别的,而用户个性化服务应该是伴生规模的。
如果人工智能技术带来的变革确实能够比拟工业革命的话,那么它势必会成就一代人,同时也淘汰掉一代人。而且,仔细想想,其实人工智能离我们并不遥远,甚至可以说已经开始深入到我们的日常生活中了。从iPhone里的Siri,到各大网站的内容推荐系统,再到图像识别和人脸识别技术的广泛应用,这些场景的背后都有这项技术在发挥作用。
作为程序员,以机器学习和深度学习为代表的人工智能技术,与我们的关系则更加紧密。现在凡是有些规模的互联网公司,基本都有专门研究算法的团队。在数据挖掘、Antispam、推荐系统和广告系统,以及其它一些领域,我们都多多少少会涉及到一些机器学习的技术。即使我们不亲自负责开发和维护这些技术,在工作中也难免会与之产生交集。
说了这么多,我其实想强调的一点是:任何人都应该了解一点跟人工智能有关的技术,因为这是无法阻挡的大潮,是不可避免的未来趋势。
而对于一名没有涉及到任何这方面技术的工程师来说,这项技术本身的独特性也绝对值得你花时间去了解。你一旦了解就会发现,这是一种全然不同的编程方式。
本文就是这样的一篇科普文章,目的是向所有没有接触过人工智能技术的程序员(甚至非技术人员),介绍人工智能领域最前沿的神经网络和深度学习方面的知识。也许,你看完之后,会像我第一次接触它们的时候一样,惊奇地感叹:这种编程方式简直是造物主留下的一个后门!竟然用如此简单的算法就能实现出远远超越原本设计的智能!
好了,蓄势完毕,相信现在你对于是否愿意花时间读完剩下的内容,已经做出自己的决定了。实际上,这项科普的工作并不轻松,因为这项技术涉及到不少数学知识。为了避免阅读障碍,我会尝试在描述的过程中尽量不引入复杂的数学公式,同时让讲解尽量有趣。
感知器
要想理解深度学习,我们就必须先理解人工神经网络,因为神经网络是深度学习的基础。而要理解神经网络,我们就必须先理解它的基本组成单元——神经元(neuron)。
感知器(perceptron)是一种早期的神经元结构,在上个世纪五六十年代就被提出来了[1]。现在它在神经网络中已很少被使用,但理解它有助于理清其它类型神经元的基本结构和设计思路。
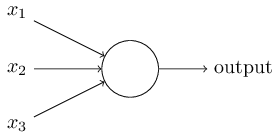
如上图所示,一个感知器的定义元素包括:
- 有多个输入:x1, x2, x3, …, 它们只能是0或1。
- 有一个输出:output. 只能是0或1。
- 每个输入对应一个权重值:w1, w2, w3, …, 它们可以是任意实数。
- 有一个阈值:threshold. 可以是任意实数。
- 输出output取决于各个输入的加权求和与阈值threshold的大小,即:如果w1x1 + w2x2 + w3x3 + … > threshold,则输出output=1,否则输出output=0。
直观上理解,感知器相当于一个决策模型。输入表示进行决策时需要考虑的外在因素或条件,权重表示你对某个外在因素的重视程度,而阈值则表示你对于这个决策事件本身的喜好程度或接受程度。
举一个例子:假设周末有一个同学聚会,现在你正在决策要不要去参加。你考虑的因素如下:
- 如果那天天气好,那么你就更有意愿去参加。用x1=1表示天气好,x1=0表示天气不好。你对于天气这个因素的重视程度为w1=3。
- 如果某个你讨厌的人也去参加聚会,那么你就兴趣索然,不太乐意去了。用x2=1表示你讨厌的那个人去参加聚会,x2=0表示那个人不参加聚会。对应权重w2=-5,负值表示这个因素的出现会降低你去参加聚会的意愿。
- 但如果你暗恋的一个女孩去参加聚会,那么你无论如何也是想去的。用x3=1表示那个女孩去参加聚会,x3=0表示她不参加聚会。这个女孩对于你太重要了,所以有一个很大的权重:w3=10。
现在假设阈值threshold=2。我们根据前面的规则去计算output,这个计算过程就相当于决策过程。如果output算出来等于1,那么你就去参加聚会,否则就不去。
决策结果无非是下面几种:
- 如果你暗恋的女孩去参加聚会,那么不管其它因素,你肯定就去了。因为权重w3实在太大了,不管另外的输入是多少,都会导致加权求和后超过threshold=2。
- 你暗恋的那个女孩不去参加聚会,而你讨厌的那个人去参加聚会。这时不管天气如何,你都不会去了。
- 你暗恋的那个女孩和你讨厌的那个人都不去参加聚会。那么你去不去最终取决于天气怎么样。
对于一个给定的感知器来说,它的权重和阈值也是给定的,代表一种决策策略。因此,我们可以通过调整权重和阈值来改变这个策略。
关于阈值threshold,这里需要指出的一点是,为了表达更方便,一般用它的相反数来表达:b=-threshold,这里的b被称为偏置(bias)。这样,前面计算输出的规则就修改为:如果w1x1 + w2x2 + w3x3 + … + b > 0,则输出output=1,否则输出output=0。
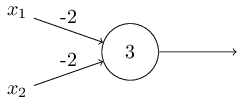
再看一下下面这个感知器。权重w1=w2=-2,而b=3。
很明显,只有当x1=x2=1的时候,output=0,因为(−2)*1+(−2)*1+3=−1,小于0。而其它输入的情况下,都是output=1。这其实是一个“与非门”!
在计算机科学中,与非门是所有门部件中比较特殊的一个,它可以通过组合的方式表达任何其它的门部件。这被称为与非门的普适性(Gate Universality)[2]。
既然感知器能够通过设置恰当的权重和偏置参数,来表达一个与非门,那么理论上它也就能表达任意其它的门部件。因此,只要创建足够多的感知器,那么它们便能够通过彼此连接从而组成一个计算机系统。但这似乎没有什么值得惊喜的,我们已经有现成的计算机了,这只不过是让事情复杂化了而已。
训练和学习
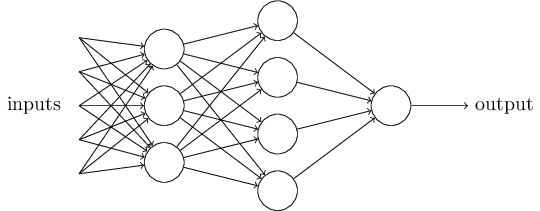
单个感知器能做的事情很有限。要做复杂的决策,我们可能需要将多个感知器连接起来。就像下面这个一样:
这个由感知器组成的网络,包含5个输入,8个感知器。权重参数的数量,我们可以算一下:5*3+3*4+4*1=31。再加上8个偏置参数,这个网络总共有39个参数。
这个图有一点需要说明的是:左边第一层的每个感知器看起来似乎有4个输出,而不是1个。但这是个错觉。实际情况是每个感知器的那唯一的一个输出分别连接到了下一层的各个感知器的输入上了。这种表示法是为了方便。输出端的多条连线只是表示连接关系,而不表示输出的个数。
这个感知器网络还算是一个简单的网络,就已经有多达39个参数了。而实际中的网络可能会有上万个,甚至数十万个参数。如果手工一个一个地去配置这些参数,恐怕这项任务永远也完成不了了。
而神经网络最有特色的地方就在于这里。我们不是为网络指定所有参数,而是提供训练数据,让网络自己在训练中去学习,在学习过程中为所有参数找到最恰当的值。
如何训练呢?大体思路是这样:我们告诉网络当输入是某个值的时候,我们期望的输出是什么。这样的每一份训练数据,称为训练样本(training example)。这个过程相当于老师在教学生某个抽象的知识的时候,举一个具体例子。一般来说,我们举的例子越多,就越能表达那个抽象的知识。这在神经网络的训练中同样成立。我们可以向网络灌入成千上万个训练样本,然后网络就自动从这些样本中总结出那份隐藏在背后的抽象的知识。这份知识的体现,就在于网络的所有权重和偏置参数的取值。
假设各个参数有一个初始值。当我们输入一个训练样本的时候,它会根据当前参数值计算出唯一的一个实际输出值。这个值可能跟我们期望的输出值不一样。想象一下,这时候,我们可以试着调整某些参数的值,让实际输出值和期望输出值尽量接近。当所有的训练样本输入完毕之后,网络参数也调整到了最佳值,这时每一次的实际输出值和期望输出值已经无限接近。这样训练过程就结束了。
假设在训练过程中,网络已经对数万个样本能够给出正确(或接近正确)的反应了,那么再给它输入一个它没见过的数据,它也应该有很大概率给出我们预期的决策。这就是一个神经网络工作的原理。
但这里还有一个问题。在训练过程中,当实际输出值和期望输出值产生差异的时候,我们如何去调整各个参数呢?当然,在思考怎么做之前,我们应该先弄清楚:通过调整参数的方式获得期望的输出,这个方法可行吗?
实际上,对于感知器网络来说,这个方法基本不可行。比如在上图有39个参数的感知器网络中,如果维持输入不变,我们改变某个参数的值,那么最终的输出基本完全不可预测。它或者从0变到1(或从1变到0),当然也可能维持不变。这个问题的关键在于:输入和输出都是二进制的,只能是0或者1。如果把整个网络看成一个函数(有输入,有输出),那么这个函数不是连续的。
因此,为了让训练成为可能,我们需要一个输入和输出能够在实数上保持连续的神经网络。于是,这就出现了sigmoid神经元。
sigmoid神经元
sigmoid神经元(sigmoid neuron)是现代神经网络经常使用的基本结构(当然不是唯一的结构)。它与感知器的结构类似,但有两个重要的区别。
第一,它的输入不再限制为0和1,而可以是任意0~1之间的实数。
第二,它的输出也不再限制为0和1,而是将各个输入的加权求和再加上偏置参数,经过一个称为sigmoid函数的计算作为输出。
具体来说,假设z=w1x1+w2x2+w3x3+…+b,那么输出output=σ(z),其中:
σ(z) = 1/(1+e-z)
σ(z)的函数曲线如下:
可见,σ(z)是一个平滑、连续的函数。而且,它的输出也是0~1之间的实数,这个输出值可以直接作为下一层神经元的输入,保持在0~1之间。
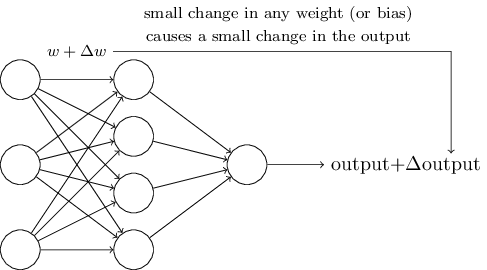
可以想象,在采用sigmoid神经元组装神经网络之后,网络的输入和输出都变为连续的了。也就是说,当我们对某个参数的值进行微小的改变的时候,它的输出也只是产生微小的改变。这样就使得逐步调整参数值的训练成为可能。这个思想如下图所示:
一个经典的应用案例
为了说明神经网络如何具体应用。这里我们引入一个经典的案例。这个例子来自Michael Nielsen的书《Neural Networks and Deep Learning》[3],是利用神经网络对于手写体数字进行识别。当然,这个例子在历史上,很多研究人员也都做过尝试。
这里顺便说一句,Michael Nielsen 的这本书真的很赞,没见过哪一份资料能把神经网络和深度学习讲解得这么透彻。这本书简直称得上是神经网络的科普圣经,感兴趣的初学者一定要读一读。
这个问题就是对类似下面这样的手写体数字进行识别,区分出它们具体是0到9哪一个数字:
这份手写体数据其实来源于一个公开的数据集,称为MNIST[4]。其中每个数字,是一张28像素×28像素的黑白图片,每个像素用一个灰度值表示。
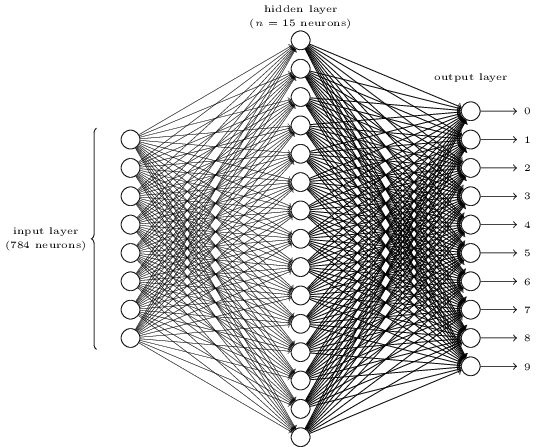
Michael Nielsen采用的神经网络结构如下:
左侧第一列圆圈表示网络的784个输入(注意图中没有画出全部),对应一张图片的28×28=784个像素点。每个像素的灰度值,在经过归一化处理之后,可以表达为0~1之间的数值,作为这里的输入。注意:这一列圆圈并不是神经元(虽然看起来像),只是输入而已。
中间一列称为隐藏层(hidden layer),图中画出的是15个神经元节点。隐藏层上的每一个节点都与每个输入连接,也就是说输入层和隐藏层之间是全连接。
这个神经网络只有一层隐藏层,属于浅层的神经网络(shallow neural networks)。而真正的深度神经网络(deep nerual networks),则会有多层隐藏层。
最右侧一列是输出层(output layer),有10个神经元节点,分别代表识别结果是0,1,2,…,9。当然,受sigmoid函数σ(z)的限制,每个输出也肯定是0~1之间的数。那我们得到一组输出值之后,我们到底认为识别结果是哪个数字呢?我们可以根据哪个输出的值最大,我们就认为识别结果就取那个数字。而在训练的时候,我们期望的输出形式是:正确的那个数字输出为1,其它输出为0。隐藏层和输出层之间也是全连接。
我们可以算一下这个神经网络共有多少个参数。权重参数有784*15+15*10=11910个,偏置参数有15+10=25个,总共参数个数为:11910+25=11935个。
对于这个神经网络的训练过程,就是要确定这11935个参数。训练的目标可以粗略概括为:对于每一个训练样本,我们期望的那个正确数字,对应的输出无限接近于1,而其它输出无限接近于0。
先不说具体的学习方法(下一节会介绍),我们先说一下神经网络这种编程方式在这一具体问题上取得的结果。根据Michael Nielsen给出的实验结果,以上述网络结构为基础,在未经过调优的情况下,可以轻松达到95%的正确识别率。而核心代码只有74行!
在采用了深度学习的思路和卷积网络(convolutional networks)之后,最终达到了99.67%的正确识别率。而针对MNIST数据集达到的历史最佳成绩是99.79%的识别率,是由Li Wan, Matthew Zeiler, Sixin Zhang, Yann LeCun, 和 Rob Fergus在2013年做出的。
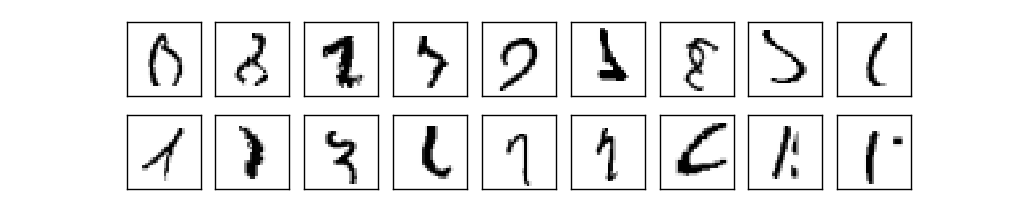
考虑到这个数据集里还有一些类似如下这样难以辨认的数字,这个结果是相当惊人的!它已经超越了真正人眼的识别了。
在本文前面一节,我们已经对神经网络的训练过程进行了描述,但其中关键的一步还没有介绍,就是如何在这个过程中一步步调整权重和偏置参数的值呢?要讲清楚这个问题,我们就必须引入梯度下降算法(gradient descent)。
随机梯度下降
在训练的过程中,我们的神经网络需要有一个实际可行的学习算法,来逐步调整参数。要设计这样一个学习算法,我们首先要明确训练的目标。
我们训练的最终目的,是让网络的实际输出与期望输出能够尽量接近。我们需要找到一个表达式来对这种接近程度进行表征。这个表达式被称为代价函数(cost function)。
一个比较常见的cost function如下所示:
这是本文出现的最复杂的一个公式了。但不用恐惧,我们对它分析一下,只要能理解它的主旨就好:
- x表示一个训练样本,即网络的输入。其实一个x代表784个输入。
- y(x)表示当输入为x的时候,期望的输出值;而a表示当输入为x的时候,实际的输出值。y(x)和a都分别代表10个输出值(以数学上的向量来表示)。而它们的差的平方,就表征了实际输出值和期望输出值的接近程度。越接近,这个差值就越小。
- n是训练样本的数量。假设有5万个训练样本,那么n就是5万。因为是多次训练,所以要除以n对所有训练样本求平均值。
- C(w,b)的表示法,是把cost function看成是网络中所有权重w和偏置b的函数。为什么这样看呢?进行训练的时候,输入x是固定的(训练样本),不会变。在认为输入不变的情况下,这个式子就可以看成是w和b的函数。那么,式子右边的w和b在哪呢?实际上,在a里面。y(x)也是固定值,但a是w和b的函数。
总结来说,C(w,b)表征了网络的实际输出值和期望输出值的接近程度。越接近,C(w,b)的值就越小。因此,学习的过程就是想办法降低C(w,b)的过程。而不管C(w,b)的表达形式如何,它是w和b的函数,这就变成了一个求函数最小值的最优化问题。
由于C(w,b)的形式比较复杂,参数也非常多,所以直接进行数学上的求解,非常困难。为了利用计算机算法解决这一问题,计算机科学家们提出了梯度下降算法(gradient descent)。这个算法本质上是在多维空间中沿着各个维度的切线贡献的方向,每次向下迈出微小的一步,从而最终抵达最小值。
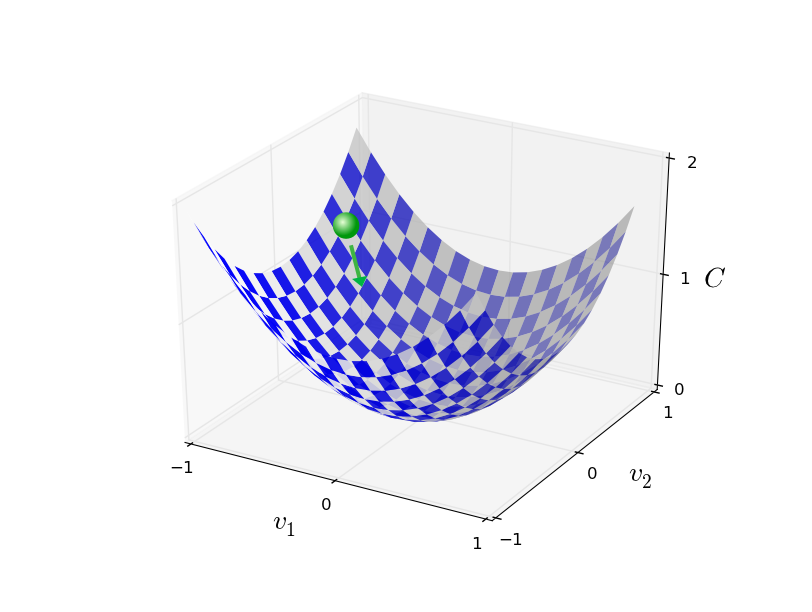
由于多维空间在视觉上无法体现,所以人们通常会退到三维空间进行类比。当C(w,b)只有两个参数的时候,它的函数图像可以在三维空间里呈现。如下所示:
就好像一个小球在山谷的斜坡上向下不停地滚动,最终就有可能到达谷底。这个理解重新推广到多维空间内也基本成立。
而由于训练样本的数量很大(上万,几十万,甚至更多),直接根据前面的C(w,b)进行计算,计算量会很大,导致学习过程很慢。于是就出现了随机梯度下降(stochastic gradient descent)算法,是对于梯度下降的一个近似。在这个算法中,每次学习不再针对所有的训练集,而是从训练集中随机选择一部分来计算C(w,b),下一次学习再从剩下的训练集中随机选择一部分来计算,直到把整个训练集用光。然后再不断重复这一过程。
深度学习
深度神经网络(具有多个hidden layer)比浅层神经网络有更多结构上的优势,它有能力从多个层次上进行抽象。
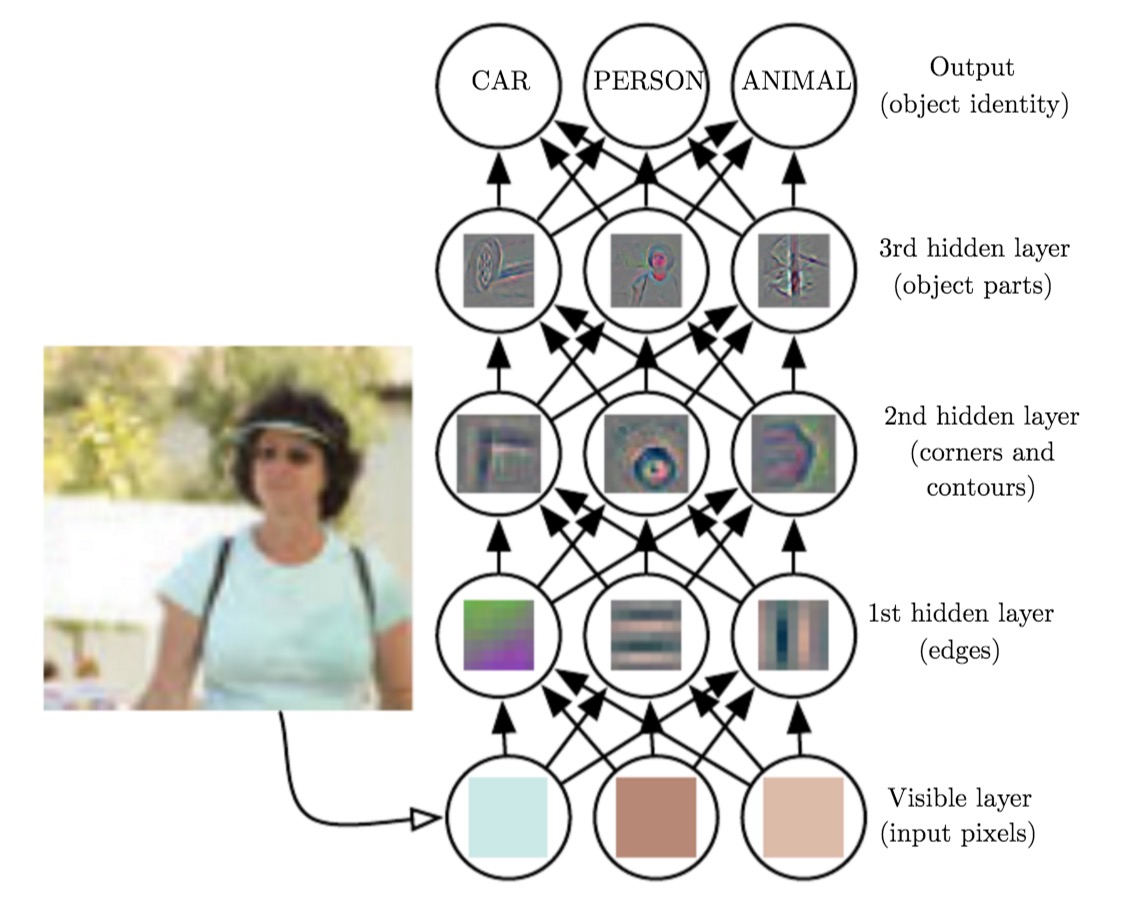
上图表达了在一个基于深度学习的图像识别过程中,逐层抽象的过程:
- 最下面的视觉输入层,接受图片的各个像素。
- 第一层hidden layer,通过比较相邻元素的不同亮度,识别出图像的边界。
- 第二层hidden layer,将边界组合,识别出图像的角和轮廓。
- 第三层hidden layer,进一步抽象,将角和轮廓进行组合,识别出物体的组成部分。
- 最终,输出层识别出具体的物体(是汽车、人,还是动物)。
从上个世纪八九十年代开始,研究人员们不断尝试将随机梯度下降算法应用于深度神经网络的训练,但却碰到了梯度消失(vanishing gradient)或梯度爆发(exploding gradient)的问题,导致学习过程异常缓慢,深度神经网络基本不可用。
然而,从2006年开始,人们开始使用一些新的技术来训练深度网络,不断取得了突破。这些技术包括但不限于:
- 采用卷积网络(convolutional networks);
- Regularization (dropout);
- Rectified linear units;
- 利用GPU获得更强的计算能力;
- 使用更好的cost function;
- ……
限于篇幅原因,我们有机会下次再讨论这些技术细节。
深度学习的优缺点
根据本文前面的介绍,深度学习的优点显而易见:这是一种全新的编程方式,它不需要我们直接为要解决的问题设计算法和编程,而是针对训练过程编程。网络在训练过程中就能自己学习到解决问题的正确方法,这使得我们可以用简单的算法来解决复杂的问题,而且在很多领域胜过了传统方法。而训练数据在这个过程发挥了更重要的作用:简单的算法加上复杂的数据,可能远胜于复杂的算法加上简单的数据。
但这项技术的一些缺点我们也不得不警惕:
- 深度网络往往包含大量的参数,这从哲学原则上不符合奥卡姆剃刀原则。通常人们要在调整这些参数上面花费巨大的精力;
- 训练深度网络需要大量的计算力和计算时间;
- 过拟合(Overfitting)问题始终伴随着神经网络的训练过程,学习过慢的问题始终困扰着人们;
- 我们很难理解神经网络的工作方式,这容易让人们产生一种失控的恐惧,同时也对这项技术在一些重要场合的进一步应用制造了障碍。
记得前一段时间在朋友圈流传甚广BetaCat的故事,讲的就是一个人工智能程序,通过自我学习,最终逐渐统治世界的故事。
那么,现在的人工智能技术的发展,会导致这种情况发生吗?会导致强人工智能的出现吗?
恐怕还不太可能。个人感觉,大概有两个重要因素:
- 第一,现在的人工智能,它的自我学习还是限定在人们指定的方式,只能学习解决特定的问题,仍然不是通用的智能。
- 第二,现在对于人工智能的训练过程,需要人们为其输入规整化的训练数据,系统的输入输出仍然对于数据的格式要求很严格。这也意味着,即使把人工智能程序连到网上,它也不能像BetaCat那样对于互联网上海量的非结构化数据进行学习。
但是,本着实用的角度,这仍然是一种非常吸引人,而且很有前景的技术。
前段时间,朋友圈里流传着另外一个故事:一个日本小伙(一位工程师)利用深度学习技术,尝试为他母亲的农场设计了分选黄瓜的机器,大大减轻了他母亲在农忙时节的工作量。
那么,同样作为工程师的你,是否也想利用平生所学,为妈妈做一点事呢?
(完)
注:本文图片素材来源[3][5]。
参考文献:
- [1] Frank Rosenblatt, http://books.google.ca/books/about/Principles_of_neurodynamics.html?id=7FhRAAAAMAAJ
- [2] Gate Universality. http://www.allaboutcircuits.com/textbook/digital/chpt-3/gate-universality/
- [3] Michael A. Nielsen, “Neural Networks and Deep Learning”, Determination Press, 2015.http://neuralnetworksanddeeplearning.com/
- [4] MNIST data set. http://yann.lecun.com/exdb/mnist/
- [5] Ian Goodfellow, Yoshua Bengio, Aaron Courville, “Deep Learning”, http://www.deeplearningbook.org/