算法中的大O表示法
1.算法概念
计算机科学中的算法指的就是计算机执行的指令。
算法是计算机处理信息的本质,因为计算机程序本质上是一个算法来告诉计算机确切的步骤来执行一个指定的任务,如计算职工的薪水或打印学生的成绩单。
一般地,当算法在处理信息时,会从输入设备或数据的存储地址读取数据,把结果写入输出设备或某个存储地址供以后再调用。
-----------
输入 --> | 算法 | --> 输出
-----------
算法的核心是创建问题抽象的模型和明确求解目标,之后可以根据具体的问题选择不同的模式和方法完成算法的设计。
2. 时间复杂度
算法的时间复杂度是指算法需要消耗的时间资源。
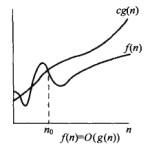
一般来说,计算机算法是问题规模n 的函数f(n),算法的时间复杂度也因此记做:
T(n) = O(f(n))
算法执行时间的增长率与f(n) 的增长率正相关,称作渐近时间复杂度(Asymptotic Time Complexity),简称时间复杂度。
3. 空间复杂度
算法的空间复杂度是指算法需要消耗的空间资源。
其计算和表示方法与时间复杂度类似,一般都用复杂度的渐近性来表示。
同时间复杂度相比,空间复杂度的分析要简单得多。
4. 大 O 表示法
- 什么是大 O 表示法?
我们常常会听到有人说,“这个算法在最糟情况下的运行时间是 O(n^2) 而且占用了 O(n) 大小的空间”,他的意思是这个算法有点慢,不过没占多大空间。
这里的O(n^2)和O(n)就是我们通常用来描述算法复杂度的大 O 表示法。
大 O 表示法能让你对一个算法的运行时间和占用空间有个大概概念。 - 大 O 表示法怎么看?怎么用?
假设一个算法的时间复杂度是 O(n),n 在这里代表的意思就是数据的个数。举个例子,如果你的代码用一个循环遍历 100 个元素,那么这个算法就是 O(n),n 为 100,所以这里的算法在执行时就要做 100 次工作。 - 大O符号是关于一个算法的最坏情况的。比如说,你要从一个大小为 100 的数组(数组中存的都是数字)中找出一个数值等于 10 的元素,我们可以从头到尾扫描一遍,这个复杂度就是 O(n),这里 n 等于 100,实际上呢,有可能第 1 次就找到了,也有可能是第 100 次才找到,但是大 O 表示法考虑的是最坏的情况,也就是一个算法理论上要执行多久才能覆盖所有的情况。
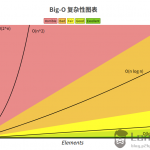
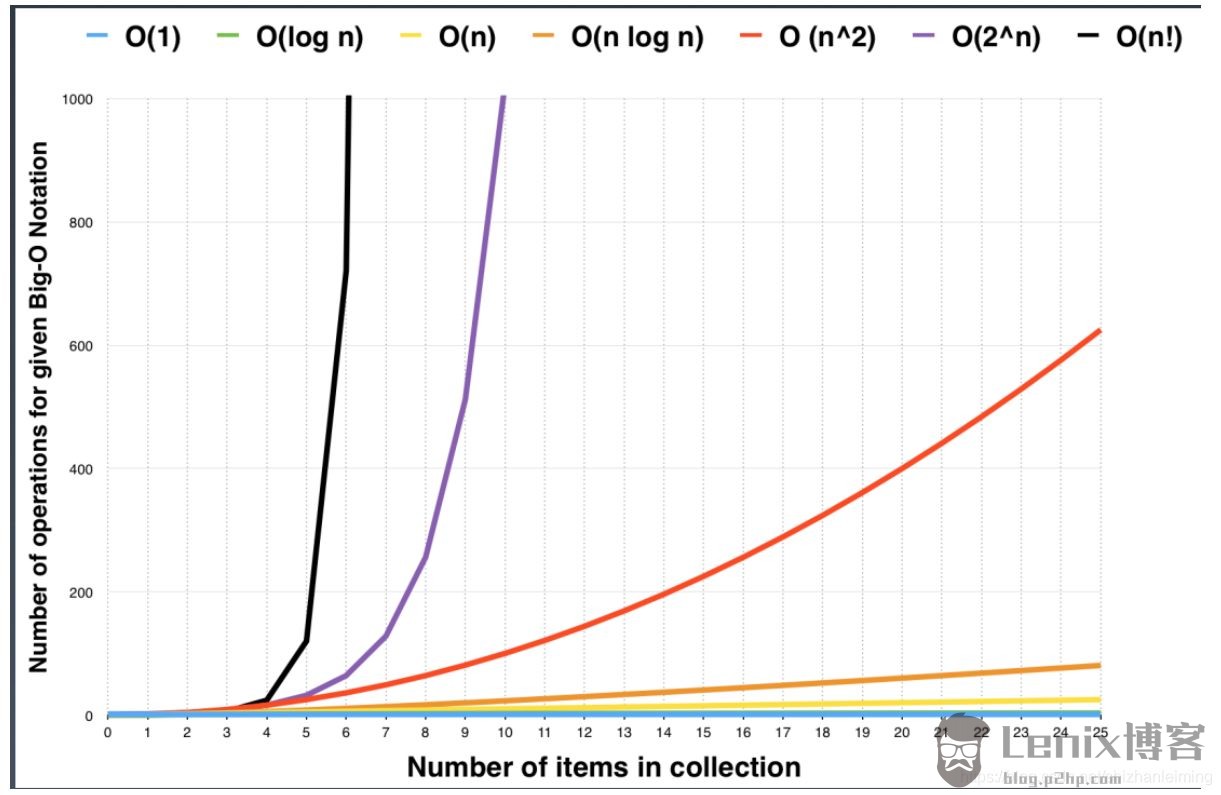
- 常见的时间复杂度有:
常数阶O(1),对数阶O(log2n),线性阶O(n),线性对数阶O(nlog2n),平方阶O(n2),立方阶O(n3),..., k次方阶O(nk),指数阶O(2n)。随着问题规模n的不断增大,上述时间复杂度不断增大,算法的执行效率越低。 - 说明:
- 大部分情况下你用直觉就可以知道一个算法的大 O 表示法
- 大 O 表示法只是一种估算,当数据量大的时候才有用
- 这种东西仅仅在比较两种算法哪种更好的时候才有点用。但归根结底,你还是要实际测试之后才能得出结论。而且如果数据量相对较小,哪怕算法比较慢,在实际使用也不会造成太大的问题。
要知道一个算法的大 O 表示法通常要通过数学分析。在这里我们不会涉及具体的数学,不过知道不同的值意味着什么会很有用。所以这里有一张方便的表。n 在这里代表的意思是数据的个数。举个例子,当对一个有 100 个元素的数组进行排序时,n = 100。
| Big-O | 名字 | 描述 |
|---|---|---|
| O(1) | 常数级 | 最好的。不论输入数据量有多大,这个算法的运行时间总是一样的。例子: 基于索引取出数组中对应的元素。 |
| O(log n) | 对数级 | 相当好。这种算法每次循环时会把需要处理的数据量减半。如果你有 100 个元素,则只需要七步就可以找到答案。1000 个元素只要十步。100,0000 元素只要二十步。即便数据量很大这种算法也非常快。例子:二分查找。 |
| O(n) | 线性级 | 还不错。如果你有 100 个元素,这种算法就要做 100 次工作。数据量翻倍那么运行时间也翻倍。例子:线性查找。 |
| O(n log n) | 线性对数级 | 还可以。比线性级差了一些,不过也没那么差劲。例子:最快的通用排序算法。 |
| O(n^2) | 二次方级 | 有点慢。如果你有 100 个元素,这种算法需要做 100^2 = 10000 次工作。数据量 x 2 会导致运行时间 x 4 (因为 2 的 2 次方等于 4)。例子:循环套循环的算法,比如插入排序。 |
| O(n^3) | 三次方级 | 特别慢。如果你有 100 个元素,那么这种算法就要做 100^3 = 100,0000 次工作。数据量 x 2 会导致运行时间 x 8。例子:矩阵乘法。 |
| O(2^n) | 指数级 | 超级慢。这种算法你要想方设法避免,但有时候你就是没得选。加一点点数据就会把运行时间成倍的加长。例子:旅行商问题。 |
| O(n!) | 阶乘级 | 比蜗牛还慢!不管干什么都要跑个 N 年才能得到结果。 |
大部分情况下你用直觉就可以知道一个算法的大 O 表示法。比如说,如果你的代码用一个循环遍历你输入的每个元素,那么这个算法就是 O(n)。如果是循环套循环,那就是 O(n^2)。如果 3 个循环套在一起就是 O(n^3),以此类推。
注意,大 O 表示法只是一种估算,当数据量大的时候才有用。举个例子,[插入排序](Insertion Sort/)的最糟情况运行时间是 O(n^2)。 理论上来说它的运行时间比[归并排序](Merge Sort/)要慢一些。归并排序是 O(n log n)。但对于小数据量,插入排序实际上更快一些,特别是那些已经有一部分数据是排序好的数组。

最后更新于 2022年6月26日