算法分析—大O、大Ω、大θ

前言

在算法的学习中，最开始便是要学习算法的分析。学习算法分析时，我们便会接触到这么几个符号：大O、大Ω、大θ，常常让人难以理解。

在通常的算法分析时，我们可以明白，在输入规模较小，各种算法之间的时间消耗并无明显差别。只有当输入规模较大时，对各个算法之间消耗差别的对比与分析才有意义。所以上面几个符号便常用于表达当规模逐渐趋向于一个极大数时的算法复杂度。

在表示一个算法时间复杂度时，我们常用如 T(n)=O(n^2) 的形式表示，而在渐进分析中的 “=” 更倾向于 “∈” 的意思。打个比方：渐进表达式 f(n) = O(g(n)) 所表达的意思是 O(g(n)) = [ f(n),h(n),…,g(n) ], f(n) ∈ O(g(n)) 。

一、大O表示法

f(x) = O(g(x)) 表示的含义是f(x)以g(x)为上界

大O是我们在分析算法复杂度时最常用的一种表示法。当函数的大小只有上界，没有明确下界的时候，则可以使用大O表示法，该渐进描述符一般用与描述算法的 最坏复杂度。f(x) = O(g(x))正式的数学定义：存在正常数c、n、n0，当 n>n0 的时，任意的 f(n) 符合 0 <= f(n) <= c.g(n)。

坐标图如下：

示例：
下面是一个很简单的嵌套循环，在分析这种简单算法的复杂度时，我们通常计算其中 关键步骤的执行次数 作为此算法的时间复杂度。
分析一： 该算法外层执行了 n 次循环，如果内层也是 n 次循环，我们便可知道该算法时间复杂度为 n^2，但是该算法内层执行的循环次数会随着外层循环的进行依次减少，最大为n。所以，我们便可以确定该算法的时间复杂度有一个上界 n^2，即T(n) = O(n^2)。
分析二： 另外我们可以采用最简单的加法来判定该算法复杂度，随着外层的循环，内层执行的次数依次为 n、n-1、…、2、1，那么关键步骤总的执行次数为等差数列的和 (n+1)*n/2, 展开即 n^2/2 + n/2，以此也可确定一个上界n^2，在我们使用O时，常有的一个说法便是“ O为取最高次数项去掉系数 ”。

	for (int i = 0; i < n; i++) {
		for (int j = i; j < n; j++) {
			...		// 关键步骤
		}
	}

 

• 1
• 2
• 3
• 4
• 5

二、大Ω表示法

f(x) = Ω(g(x)) 表示的含义是f(x)以g(x)为下界

当函数的大小只有下界，没有明确的上界的时候，可以使用大Ω表示法，该渐进描述符一般用与描述算法的 最优复杂度 。 f(n)= Ω(g(n)) 正式的数学定义：存在正常数c、n、n0，当 n > n0 的时，任意的 f(n) 符合 0 <= c.g(n) <= f(n)。

坐标图如下：

简析：
为什么我们通常把O用于分析最坏复杂度，把Ω用于分析最优复杂度？
大Ω描述的界是渐进最小，加入用大Ω来描述最坏复杂度，因为这只是一个下界，并不能说明算法的最坏复杂度，所以没意义。大O同理。

三、大θ表示法

f(x) = Θ(g(x)) 表示的含义是g(x)是f(x)的确界

用于界定函数的渐进上界和渐进下界。当 f(n)= θ(g(n)) 的时候，代表着g(n)为f(n)的渐进紧确界。而θ渐进描述符在所有的渐进描述符中是最严格的一个，因为它既描述了函数的上界，有描述了函数的下界。
f(n)= θ(c.g(n)) 正式的数学定义：存在正常数c1、c2、n、n0，当 n > n0 的时，对于任意的f(n）对符合 c1.g(n) <= f(n) <= c2.g(n)，c1.g(n)、c2.g(n)都是渐进正函数（当n趋于无穷大的时候，f(n)为正）。

坐标图如下：

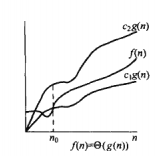
算法导论中还根据大O，大Ω，大θ的定义得到以下定理：
当且仅当函数 f(n) = O(g(n)) 并且 f(n）= Ω(g(n)) 时，才有 f(n) = θ(g(n))。

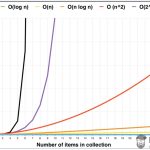
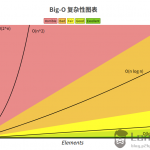
常见的几个算法复杂度

上图横轴代表输入规模，数轴代表复杂度，由图中的时间复杂度增长趋势可以看出:

• 常见的最优的算法复杂度为logN；
• 当 N 的值较小时，NlogN < N, 当 N 的值较大时，NlogN > N；
• 指数次方与阶乘的复杂度非常高，应当尽量避免使用这些算法，二次方或三次方的时间复杂度在N值较大是也是相当高的，在设计算法的时候必须要注意这一点；

参考博文：
算法分析与时间复杂度
算法分析——算法的渐进效率分析 和 渐进符号大O、大Ω、大θ、小o、小ω